SRTM DEM destriping with SAGA GIS: consequences on drainage network extraction.
Alessandro Perego
January 2009
Abstract. The SRTM (Shuttle Radar Topography Mission) DEMs present a random noise and a striping error which are negligible in mountainous zones but significant in the flat areas where their magnitude is comparable with the real topographic gradient. This works shows how to filter the DEM in order to reduce the vertical errors avoiding the loss of the real morphological details. The procedure is similar to the method proposed by Oimoen [4] but it can be used also for oblique striping.
The consequences of the destriping on the extraction of the drainage network are showed. The fluvial network from DEM is compared with that one from satellite imagery in order to evaluate the improvement of the DEM after the destriping.
The whole work is made with free or open-source software and some modules for SAGA GIS have been realized.
Key words: DEM, destriping.
Introduction
The SRTM (Shuttle Radar Topography Mission, http://srtm.usgs.gov/) digital elevation models are freely available data useful in geomorphological studies at medium scale. They are produced by radar interferometry on data from SIR-C and X-SAR instruments on board of Space Shuttle Endeavour in February 2000 during the STS-99 mission [2; 3; 5; 8]. This mission saw the collaboration among the National Aeronautics and Space Administration (NASA), the National Imagery and Mapping Agency (NIMA, nowadays renamed National Geospatial-Intelligence Agency, NGA), the Deutschen Zentrum für Luft- und Raumfahrt (DLR) and the Agenzia Spaziale Italiana (ASI) and produced a near-global elevation model covering the 80% of Earth surfaces. The vertical absolute error is less than 16 m and the relative one is less than 10 m, for 90% of the data [6]. Berry et al. calculated a mean global difference with radar altimetry data equal to 3.60 m [1].
The "finished" version of the level SRTM3, with spatial resolution equal to 3 arc-second (about 90 m on the Equator), was used during a geomorphological study of a low relief area in north-eastern Syria. As the area is semiarid with poor arboreal vegetation the DEM is also a DTM, but two kind of error was noticed: a random noise and a double oblique striping. The magnitude of these errors is low (few meters) but in weak relief areas it is higher than the real topographic gradient between adjacent pixels so it falsifies the surface exposure invalidating the qualitative and quantitative analyses.
This work suggests a method to fade out the errors without losing real morphological details such as the large artificial mounds attributable to the Bronze Age called "tells" [7].
Software and methods
SAGA (System for Automated Geoscientific Analysis) GIS version 2.0 RC3 by the University of Goettingen (http://www.saga-gis.uni-goettingen.de/) was used to analyse and process the DEM.
The magnitude of the random errors seems to be less than 2 m (fig. 1). In order to eliminate this noise a specific raster filter was written in C++ and compiled with Microsoft Visual C++ 2005 Express Edition (http://msdn.microsoft.com/vstudio/express/visualc/). It calculates, for each pixel, the average of the values within a distance of 2 cells but using only the cell's values differing from the central one less than 2 m and giving more weight to the nearer cells. This allows eliminating most of the random noise without smoothing many real topographic details.
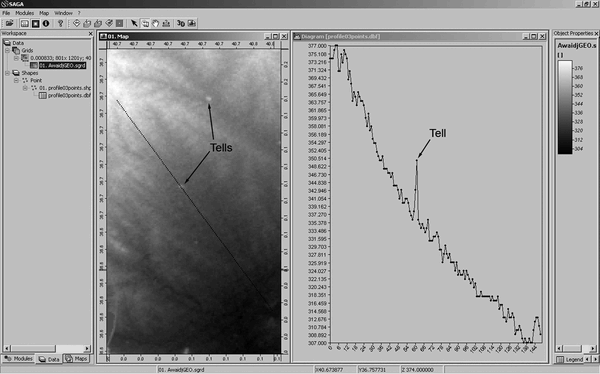
Figure
1. Example of profile used to determine the magnitude's threshold
between the noise and the real topographic features. It seems to be
about 2 m
The other significant source of errors consist of two series of stripes with inclination 32,5° and -32,5° regarding the horizontal (fig. 2).

Figure 2. NE-SW striping in a low relief area.
A destriping module with the following algorithm was created (it works for striping angle between -45° and +45°):
Cdestriping::Cdestriping(void)
{
Parameters.Add_Grid(NULL, "INPUT", _TL("Input"), _TL("This must be your input data of type grid."), PARAMETER_INPUT);
Parameters.Add_Grid(NULL, "RESULT3", _TL("Destriped Grid"), _TL("New grid filtered with the destriping module"), PARAMETER_OUTPUT);
Parameters.Add_Grid(NULL, "RESULT1", _TL("Low-pass 1"), _TL("Step 1: low-pass of stripe"), PARAMETER_OUTPUT);
Parameters.Add_Grid(NULL, "RESULT2", _TL("Low-pass 2"), _TL("Step 2: low-pass between stripe and its surruondings"), PARAMETER_OUTPUT);
Parameters.Add_Value(NULL, "ANG", _TL("Angle (in degrees)"), _TL("0 is horizontal, 90 is vertical."), PARAMETER_TYPE_Double, 0.0);
Parameters.Add_Value(NULL, "R", _TL("Radius"), "", PARAMETER_TYPE_Double, 20);
Parameters.Add_Value(NULL, "D", _TL("Stripes width"), "", PARAMETER_TYPE_Double, 2);
}
Cdestriping::~Cdestriping(void)
{}
bool Cdestriping::On_Execute(void)
{
int x, y, r, dxmax, dymax, ix, ax, ay, bx, by, iy, iv, iw, n1, n2;
double z, iz, d, ang, a, si, si2, co, co2, Sum1, Sum2;
CSG_Grid *pInput, *pRes1, *pRes2, *pRes3;
pInput = Parameters("INPUT")->asGrid();
pRes1 = Parameters("RESULT1")->asGrid();
pRes2 = Parameters("RESULT2")->asGrid();
pRes3 = Parameters("RESULT3")->asGrid();
ang = Parameters("ANG")->asDouble();
r = Parameters("R")->asInt();
d = Parameters("D")->asDouble();
a = ang * 6.283185307179586 / 360;
si = sin(a);
co = cos(a);
si2 = si * si;
co2 = co * co;
dxmax = (r*sqrt(co2))+(d/2*sqrt(si2));
dymax = (r*sqrt(si2))+(d/2*sqrt(co2));
if(si2 < co2)
{
double sico, co05, dco, ivsico, iwmin1, iwmax1, iwmin2, iwmax2;
sico = si / co;
co05 = sqrt( (0.5/co)*(0.5/co) );
dco = sqrt( (d/2/co)*(d/2/co) );
for(y=0; y<Get_NY() && Set_Progress(y); y++)
{
for(x=0; x<Get_NX(); x++)
{
Sum1 = 0.0;
n1 = 0;
Sum2 = 0.0;
n2 = 0;
if( (ax = x - dxmax) < 0 ) {ax = 0;}
if( (bx = x + dxmax) >= Get_NX() ) {bx = Get_NX() - 1;}
if( (ay = y - dymax) < 0 ) {ay = 0;}
if( (by = y + dymax) >= Get_NY() ) {by = Get_NY() - 1;}
for(ix=ax; ix<=bx; ix++)
{
iv = x - ix;
ivsico = iv * sico;
iwmin1 = ivsico - co05;
iwmax1 = ivsico + co05;
iwmin2 = ivsico - dco;
iwmax2 = ivsico + dco;
for(iy=ay; iy<=by; iy++)
{
iw = y - iy;
if( iw >= iwmin1 && iw <= iwmax1)
{
iz = pInput->asDouble(ix, iy);
Sum1 += iz;
n1++;
}
if( iw >= iwmin2 && iw <= iwmax2)
{
iz = pInput->asDouble(ix, iy);
Sum2 += iz;
n2++;
}
}
}
if( n1 > 0 && n2 > 0 )
{
pRes1->Set_Value(x, y, Sum1/n1);
pRes2->Set_Value(x, y, Sum2/n2);
z=pInput->asDouble(x, y);
pRes3->Set_Value(x, y, (Sum2/n2)-(Sum1/n1)+z);
}
}
}
}
return( true );
}
The module asks the striping angle (ang), the filtering radius (r) which should be half of the maximum length in pixels of the visible stripes and the width (d) in pixel of the stripes. In this case the modules was applied twice using 32.5 and -32.5 as striping angle, 100 as filtering radius and 9 as stripe's width.
In the first pass the filter calculates the average altitude along the direction of the striping therefore, in the second pass, it computes the average between the stripes in relief and the depressed ones. The difference between the values obtained in the two passes is statistically the striping error and it can be removed from the original DEM. The method is substantially similar to that one proposed by Oimoen for horizontal or vertical striping [4] but it can be applied to oblique striping.
Using the modules already included in SAGA GIS the "cleaned" DEM and the original one were converted in UTM projection, zone 37N, they were pre-processed to remove the holes (Sink removal), and the drainage network was extracted using both a unidirectional algorithm (Deterministic 8) and a multidirectional one (Multiple Flow Direction).
A SPOT 5 (©CNES, 2006 - Spot Image) panchromatic scene with spatial resolution 2.5 m, acquired in July 2006, was obtained thanks to the O.A.S.I.S. program (http://medias.obs-mip.fr/oasis/) and a panchromatic images DOI-10M with spatial resolution 10 m, deriving from SPOT images acquired between years 1992 and 1994, was obtained from the National Geospatial-Intelligence Agency (NGA) Raster Roam (http://geoengine.nima.mil/geospatial/
SW_TOOLS/NIMAMUSE/webinter/rast_roam.html). These images were elaborated with OSSIM (Open Source Software Image Map, http://www.ossim.org/OSSIM/Welcome.html) to convert them in UTM projection and high-pass filters were applied to contrast the fluvial traces.
The open source gvSIG (http://www.gvsig.gva.es/index.php?id=gvsig&L=2) software was use to draw as shapefile the drainage recognizable in satellite imagery. This shapefile was imported in SAGA GIS and it was compared with the automatically extracted drainage.
Result and conclusion
After removing the random noise and destriping, the real topographical details such as "tells" are better legible on the DEM (fig. 3). Also the derived images of slope and aspect are cleaner. In particular the slope values in the valley bottoms are lower (fig. 4).
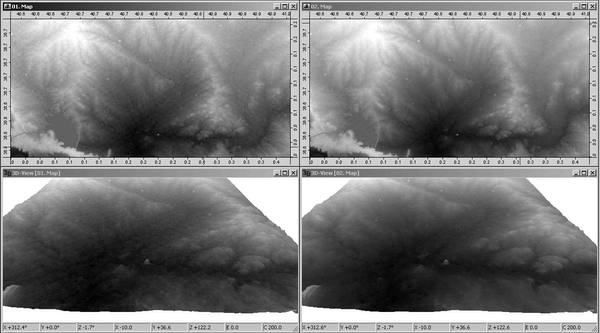
Figure 3. The DEM before (on the left) and after (on the right) the destriping procedure.
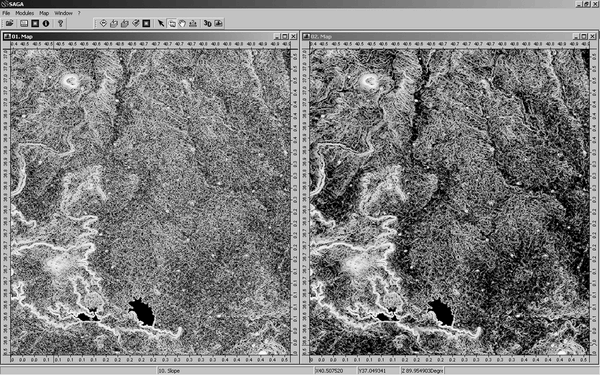
Figure 4. The slopes calculated from the DEM before (on the left) and after (on the right) the destriping. The steeper slopes are brighter, the flat areas are darker.
The striping in a DEM creates a series of linear parallel ridges and depressions which falsify the water flow. The drainage network gained from the destriped DEM agrees better with that one reconstructed from the satellite imagery (fig. 5) demonstrating that the proposed method allows an extraction more adherent to the reality. In one case the drainage extracted from the "clean" DEM differs remarkably from the visible channels in SPOT 5. In correspondence of the automatically extracted feature the older DOI-10M image shows a faint fluvial trace completely deleted in the more recent images (fig. 6). Maybe the DEM allowed getting an ancient natural stream which was recently diverted.
Whether with a unidirectional algorithm or with a multidirectional one the differences in the drainage's extraction between the original DEM and the destriped one are substantially the same. However the Multiple Flow Direction method allows characterizing the areas of uncertainty where it draws blurred flow ways.
Therefore the proposed method determines an effective improvement of the DEM. The drainage network extracted from the DEM and compared with the satellite imagery may be useful for example in geomorphological studies in order to recognize the position of palaeo-rivers in semiarid areas.
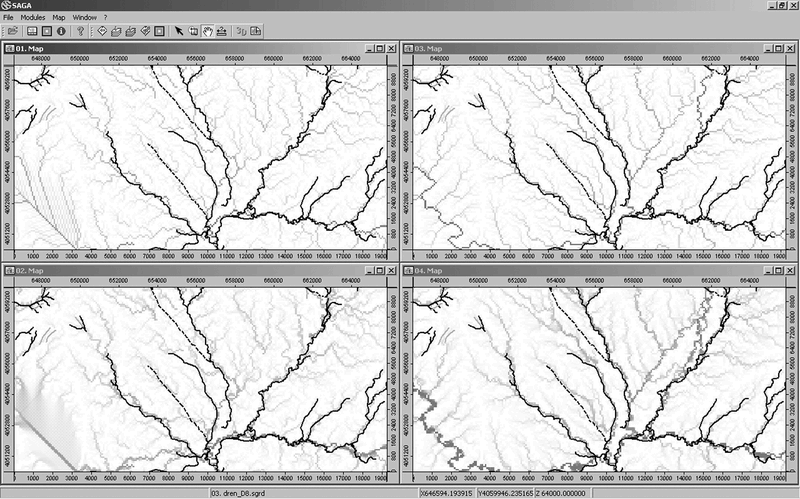
Figure 5. Comparison between the drainage network extracted from DEM (in grey) and the fluvial traces visible in SPOT 5 imagery (in black, the dashed lines are artificial channels). 01 Map: Deterministic 8 algorithm before the destriping; 02 Map: Multiple Flow Direction algorithm before the destriping; 03 Map: Deterministic 8 algorithm after the destriping; 04 Map: Multiple Flow Direction algorithm after the destriping.
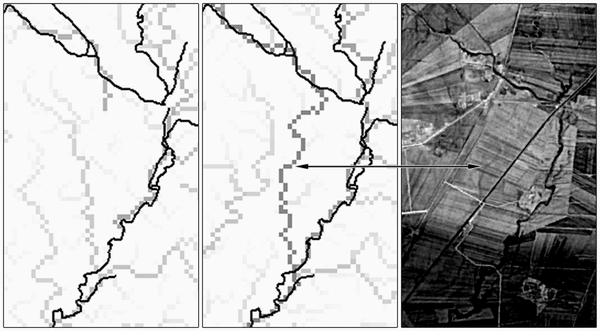
Figure 6. Comparison between the drainage extracted from DEM (grey lines) before (on the left) and after (on the centre) the destriping. The post-destriping extraction shows a line visible in DOI-10M imagery (on the right) but not in more recent SPOT 5 images.
References
1. P.A.M. Berry, J.D.Garlick, R.G. Smith. "Near-global validation of the SRTM DEM using satellite radar altimetry", Remote Sensing of Environment, Vol. 106:17-27, 2007
2. T.G. Farr, M. Kobrick. "Shuttle Radar Topography Mission produces a wealth of data", Amer. Geophys. Union Eos, Vol. 81:583-585, 2000
3. T.A. Hennig, J.L. Kretsch, C.J. Pessagno, P.H. Salamonovicz, W.L. Stein. "The Shuttle Radar Topography Mission", in Lecture Notes In Computer Science, 2181, Proceedings of the First International Symposium on Digital Earth Moving, C.Y. Westort (ed.), Springer-Verlag: London, 2001, pp. 65-77,
4. M.J. Oimoen. "An Effective Filter For Removal Of Production Artifacts In U.S. Geological Survey 7.5-Minute Digital Elevation Models", in Proceedings of the Fourteenth International Conference on Applied Geologic Remote Sensing, Las Vegas, NV, USA, 2000.
5. B. Rabus, M. Eineder, A. Roth, R. Bamler. "The shuttle radar topography mission-a new class of digital elevation models acquired by spaceborne radar", ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 57: 241-262, 2003.
6. E. Rodriguez, C.S. Morris, J.E. Belz, E.C. Chapin, J.M. Martin,W. Daffer, S. Hensley, "An assessment of the SRTM topographic products", Jet Propulsion Laboratory, Pasadena, California, Technical Report JPL D-31639, 2005.
7. A, Sherratt. "Spotting tells from space", Antiquity, Vol. 78, on-line article http:// www.antiquity.ac.uk/projgall/sherratt/ , 2004,
8. J.J. Van Zyl. "The Shuttle Radar Topography Mission (SRTM): a Breakthrough in Remote Sensing of Topography", Acta Astronautica, Vol. 48: 559-565, 2001.
| Argomenti correlati: |
| >>> SAGA |
| >>> SRTM DEM |
| >>> Average filters for SAGA |